Задание №205
Условие
В правильном тетраэдре SABC на ребре AC взята точка F так, что AF:FC=2:1.
а) Постройте сечение тетраэдра плоскостью, проходящей через точки B, F и высоту грани BSC, проведенную к ребру SC.
б) Найдите расстояние от точки F до плоскости BSC, если ребро тетраэдра равно 12.
Решение
а) В треугольнике BSC проведем высоту BE. Соединим точки B, E и F. \bigtriangleup BEF — искомое сечение.
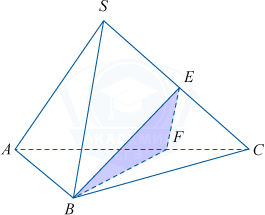
б) 1) Изобразим тетраэдр так, как показано на рисунке ниже:
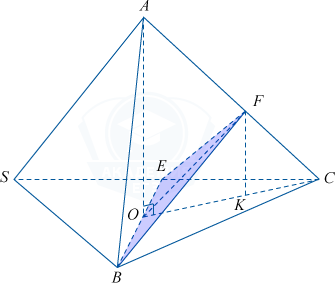
Пусть AO — высота правильного тетраэдра ABCS, AO\perp (BSC). Так как тетраэдр правильный то O — центр описанной окружности \bigtriangleup BCS, CO — ее радиус, CO=\frac{a\sqrt{3}}{3}, где a=12 — сторона правильного треугольника SBC, CO =4\sqrt{3}.
2) \bigtriangleup CAO — прямоугольный, \angle AOC=90^{\circ}. По теореме Пифагора AO=\sqrt{AC^2-CO^2}=\sqrt{144-48}=4\sqrt{6}.
3) Пусть FK\perp CO. Тогда FK \parallel AO, AO\perp (BSC), следовательно, FK\perp (BSC). Значит, FK — искомое расстояние.
4) Заметим, что \bigtriangleup FCK \sim \bigtriangleup AOC по двум углам (\angle FKC=\angle AOC=90^{\circ}, \angle C — общий), тогда \frac{FK}{AO}=\frac{FC}{AC}=\frac{FC}{FC+AF}. Учитывая, что по условию AF=2FC, получаем \ \frac{FK}{AO}=\frac{FC}{FC+2FC}=\frac{1}{3}, FK=\frac{AO}{3}=\frac{4\sqrt{6}}{3}.
Ответ
\frac{4\sqrt{6}}{3}