Задание №220

а) Рассмотрим треугольную пирамиду D_1ACD.

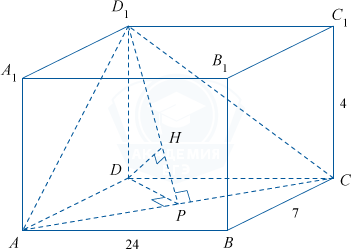
В данной пирамиде расстояние от точки D до плоскости основания ACD_1-DH — равно высоте пирамиды, проведенной из точки D, к основанию ACD_1.

V_{D_1ABC}=\frac1{3}S_{ACD_1} \cdot DH, из этого равенства получаем

DH=\frac{3V_{D_1ACD}}{S_{ACD_1}}.

Рассмотрим пирамиду D_1ABC. Расстояние от точки B до плоскости ACD_1 равно высоте, опущенной из вершины B к основанию ACD_1. Обозначим это расстояние BK. Тогда V_{D_1ABC}=\frac1{3}S_{ACD_1} \cdot BK, из этого получаем BK=\frac{3V_{D_1ABC}}{S_{ACD_1}}.\: Но V_{D_1ACD} = V_{D_1ABC}, так как, если считать в пирамидах основаниямиADC и ABC, то высота D_1D общая и S_{ADC}=S_{ABC} (\bigtriangleup ADC=\bigtriangleup ABC по двум катетам). Значит, BK=DH.

б) Найдем объем пирамиды D_1ACD.

Высота D_1D=4.

S_{ACD}=\frac1{2}AD \cdot DC=\frac1{2} \cdot24 \cdot 7=84.

V=\frac1{3}S_{ACD} \cdot D_1D=\frac1{3} \cdot84 \cdot4=112.

Площадь грани ACD_1 равна \frac1{2}AC \cdot D_1P.

AD_1= \sqrt{AD^{2}+DD_1^{2}}= \sqrt{7^{2}+4^{2}}= \sqrt{65}, \: AC= \sqrt{AB^{2}+BC^{2}}= \sqrt{24^{2}+7^{2}}= 25

Зная, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла, в треугольнике ADC имеем AD^{2}=AC \cdot AP, \: AP=\frac{AD^{2}}{AC}=\frac{7^{2}}{25}=\frac{49}{25}.

В прямоугольном треугольнике AD_1P по теореме Пифагора D_1P^{2}= AD_1^{2}-AP^{2}= 65-\left ( \frac{49}{25} \right )^{2}= \frac{38\:224}{25^{2}}, D_1P=\frac{4\sqrt{2\:389}}{25}.

S_{ACD_1}=\frac1{2} \cdot25 \cdot\frac{4\sqrt{2\:389}}{25}=2\sqrt{2\:389}.

DH=\frac{3V}{S_{ACD_1}}=\frac{3 \cdot112}{2\sqrt{2\:389}}=\frac{168}{\sqrt{2\:389}}.

\frac{168}{\sqrt{2\:389}}