Задание №966

а) Плоскости MNK и DBC параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Докажем это. Рассмотрим прямые MN и KM плоскости MNK и прямые BC и DB плоскости DBC.

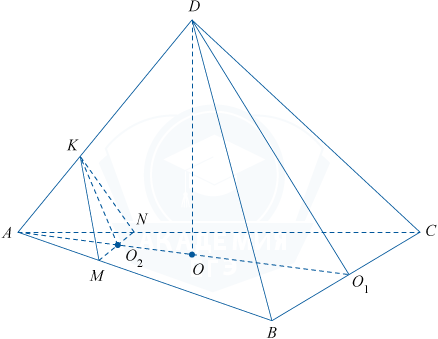
В треугольнике AOD: \angle AOD = 90^\circ и по теореме Пифагора AD=\sqrt{DO^2 +AO^2}.

Найдём AO, используя то, что \bigtriangleup ABC правильный.

AO=\frac{2}{3}AO_1, где AO_1 — высота \bigtriangleup ABC, AO_1 = \frac{a\sqrt{3}}{2}, где a — сторона \bigtriangleup ABC.

AO_1 = \frac{6\sqrt{3} \cdot \sqrt{3}}{2}=9, тогда AO=6, AD=\sqrt{8^2 + 6^2}=10.

1. Так как \frac{AK}{AD}=\frac{5}{2} : 10=\frac{1}{4}, \frac{AM}{AB}=\frac{3\sqrt{3}}{2} : 6\sqrt{3}=\frac{1}{4} и \angle DAB — общий, то \bigtriangleup AKM \sim ADB.

Из подобия следует, что \angle AKM = \angle ADB. Это соответственные углы при прямых KM и BD и секущей AD. Значит KM \parallel BD.

2. Так как \frac{AN}{AC}=\frac{3 \sqrt{3}}{2 \cdot 6 \sqrt{3}}=\frac{1}{4}, \frac{AM}{AB}=\frac{1}{4} и \angle CAB — общий, то \bigtriangleup ANM \sim \bigtriangleup ACB.

Из подобия следует, что \angle ANM = \angle ACB. Эти углы соответственные при прямых MN и BC и секущей AC. Значит, MN \parallel BC.

Вывод: так как две пересекающиеся прямые KM и MN плоскости MNK соответственно параллельны двум пересекающимся прямым BD и BC плоскости DBC, то эти плоскости параллельны — MNK \parallel DBC.

б) Найдём расстояние от точки K до плоскости BDC.

Поскольку плоскость MNK параллельна плоскости DBC, то расстояние от точки K до плоскости DBC равно расстоянию от точки O_2 до плоскости DBC и оно равно длине отрезка O_2 H. Докажем это.

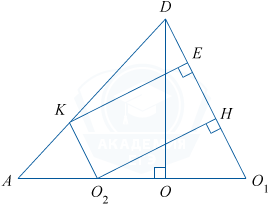
BC \perp AO_1 и BC \perp DO_1 (как высоты треугольников ABC и DBC), значит, BC перпендикулярна плоскости ADO_1, и тогда BC перпендикулярна любой прямой этой плоскости, например, O_2 H. По построению O_2H\perp DO_1, значит, O_2H перпендикулярна двум пересекающимся прямым плоскости BCD, и тогда отрезок O_2 H перпендикулярен плоскости BCD и равен расстоянию от O_2 до плоскости BCD.

В треугольнике O_2HO_1:O_2H=O_{2}O_{1}\sin\angle HO_{1}O_{2}.

O_{2}O_{1}=AO_{1}-AO_{2}.\, \frac{AO_2}{AO_1}=\frac{1}{4}, AO_{2}=\frac{AO_1}{4}=\frac{9}{4}.

O_{2}O_{1}=9-\frac{9}{4}=\frac{27}{4}.

\sin \angle DO_{1}A= \frac{DO}{DO_{1}}= \frac{8}{\sqrt{64+3^2}}= \frac{8}{\sqrt{73}}.

O_2H=\frac{27}{4} \cdot \frac{8}{\sqrt{73}}=\frac{54}{\sqrt{73}}.

\frac{54}{\sqrt{73}}