Задания по теме «Параллелограмм»

Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне, поэтому большая высота проведена к меньшей стороне. Проведём высоту DH к меньшей стороне и рассмотрим треугольник ADH.

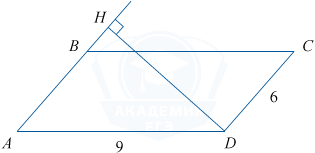
\sin A=\frac{DH}{AD}. Получаем: DH=AD\sin A= 9\cdot\frac23= 6.

Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне S = ah_a. Найдём высоты параллелограмма: h_1 = 60 : 8 = 7,5, h_2 = 60 : 12 = 5. Меньшая высота этого параллелограмма равна 5.

Точка P — середина стороны BC, поэтому PC=0,5BC. Обозначим h высоту параллелограмма, проведённую к стороне AD.

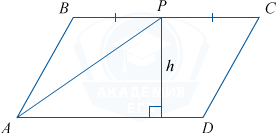
Тогда площадь параллелограмма S равна BC\cdot h=324.

Площадь трапеции APCD равна \frac{PC+AD}{2}\cdot h= \frac{0,5BC+BC}{2}\cdot h= \frac{1,5BC}{2}\cdot h= 0,75S=243

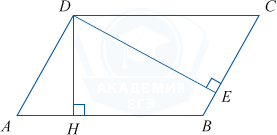
Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне. Для параллелограмма ABCD выполняется S=AB\cdot DH=CB\cdot DE. Получаем 16DH=8\cdot14, DH=7.

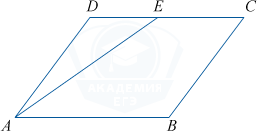
S_{ADE}=\frac{DE\cdot AM}{2},  AM\perp DC

S_{ABCD}=AB\cdot AM,  AB=2DE.

AB\cdot AM=284,  2DE\cdot AM=284.

DE\cdot AM=142,  S_{ADE}=\frac{142}{2}=71.