Задание №892
Условие
Площадь параллелограмма ABCD равна 324. Точка P — середина стороны BC. Найдите площадь трапеции APCD.
Решение
Точка P — середина стороны BC, поэтому PC=0,5BC. Обозначим h высоту параллелограмма, проведённую к стороне AD.
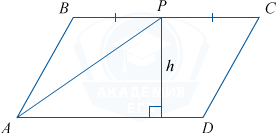
Тогда площадь параллелограмма S равна BC\cdot h=324.
Площадь трапеции APCD равна \frac{PC+AD}{2}\cdot h= \frac{0,5BC+BC}{2}\cdot h= \frac{1,5BC}{2}\cdot h= 0,75S=243
Ответ
243
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.