Задания по теме «Конус»

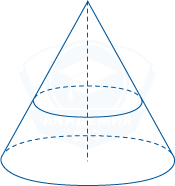
Объем большого конуса вычисляется по формуле: V_1=\frac13\pi R^2H

По условию известно, что сечение проведено через середину высоты большого конуса. Это означает, что высота и радиус основания малого конуса в 2 раза меньше высоты и радиуса основания большого конуса. Найдем объем малого конуса:

V_2=\frac13\pi r^2h=\frac13\pi\left (\frac{R}{2} \right )^2\frac{H}{2}=\frac13\pi R^2H\cdot\frac{1}{8}=\frac{V_1}{8} 

Значит объем малого конуса в 8 раз меньше объема большого и равен: \frac{32}{8}=4

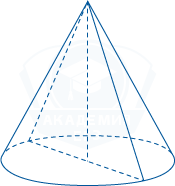
Площадь сечения вычисляется по формуле: S = ah, где:

a – половина сечения основания конуса

h – высота конуса

Найдем по теореме Пифагора половину основания:

a = 17^2-15^2=\sqrt{289-225}=\sqrt{64}=8

Найдем искомую площадь сечения:

S = 8 \cdot 15 = 120