Задание №303
Условие
На рисунке изображен график y=f'(x) производной функции f(x), определенной на интервале (-7; 5). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=3x-3 или совпадает с ней.
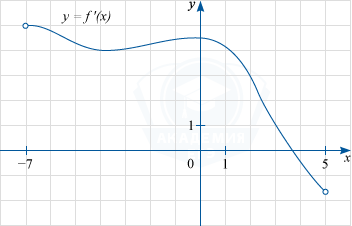
Решение
Если касательная параллельна прямой y=3x-3 или совпадает с ней, то ее угловой коэффициент равен угловому коэффициенту прямой, то есть 3.
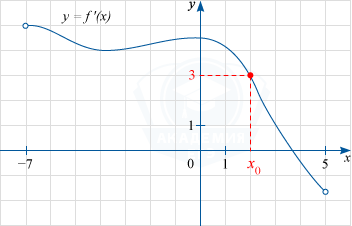
Согласно геометрическому смыслу производной это означает, что f'(x_0)=3, где x_0 — искомая абсцисса точки касания. Из данного графика производной y=f'(x) видно, что x_0=2.
Ответ
2
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.