Открытый банк заданий по теме вписанная окружность. Задания B6 из ЕГЭ по математике (профильный уровень)
Основание равнобедренного треугольника равно 12, а боковые стороны равны 10. Найдите радиус вписанной в него окружности.
Известно, что радиус r окружности, вписанной в треугольник, вычисляется по формуле r=\frac{S}{p}, где S — площадь треугольника, p — его полупериметр.
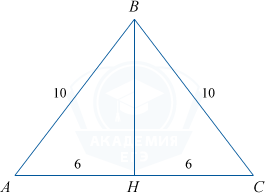
Пусть BH медиана равнобедренного треугольника, проведенная к основанию, тогда BH является высотой. По теореме Пифагора BH=\sqrt{10^2-6^2}=\sqrt{64}=8.
S=\frac12 ah=\frac12\cdot12\cdot8=48,
p=\frac{10+10+12}{2}=16,
r=\frac{48}{16}=3.
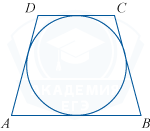
Окружность вписана в трапецию и имеет радиус 2. Найдите высоту трапеции.
.png)
Высота трапеции равна диаметру вписанной окружности:
h=d=2r=4
В четырехугольник ABCD вписана окружность. Стороны AB = 7, BC = 5, CD = 20. Найдите четвертую сторону четырехугольника AD.
Если в четырехугольник вписана окружность, значит сумма его противоположных сторон равна, т.е.:
AB + CD = AD + BC
Найдем сторону AD:
AD=AB+CD-BC=7+20-5=22
Закажите обратный звонок!