Задание №298
Условие
Основание равнобедренного треугольника равно 12, а боковые стороны равны 10. Найдите радиус вписанной в него окружности.
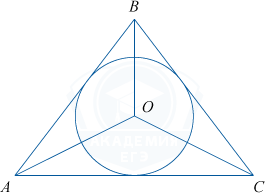
Решение
Известно, что радиус r окружности, вписанной в треугольник, вычисляется по формуле r=\frac{S}{p}, где S — площадь треугольника, p — его полупериметр.
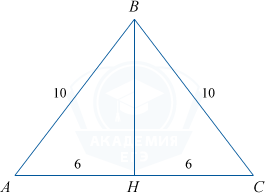
Пусть BH медиана равнобедренного треугольника, проведенная к основанию, тогда BH является высотой. По теореме Пифагора BH=\sqrt{10^2-6^2}=\sqrt{64}=8.
S=\frac12 ah=\frac12\cdot12\cdot8=48,
p=\frac{10+10+12}{2}=16,
r=\frac{48}{16}=3.
Ответ
3
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.