Открытый банк заданий по теме угол между прямой и плоскостью. Задания C2 из ЕГЭ по математике (профильный уровень)
На рёбрах AD и BD правильного тетраэдра DABC взяты точки M и K соответственно так, что MD:AM=BK:KD=2.
а) Пусть L — точка пересечения прямой KM с плоскостью ABC. Докажите, что AB:AL=3.
б) Найдите угол между прямой KM и плоскостью ABC.
а) План решения.
1. Выполним схематический чертёж.
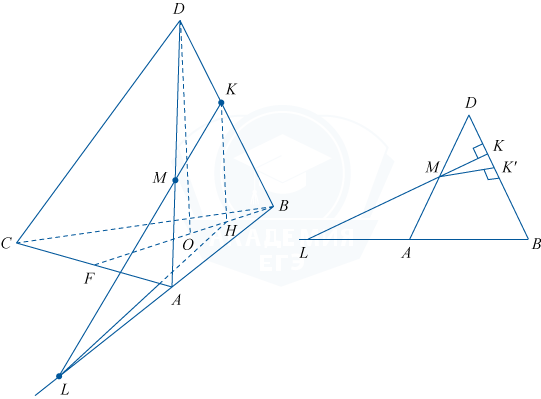
2. Сделаем предположение, что MK \perp BD, и докажем это утверждение (например, методом «от противного»).
3. Обозначим ребро тетраэдра какой-нибудь буквой (например, a) и через неё выразим другие величины.
4. Рассмотрим треугольник AML, найдём его углы. Из равенства \angle AML=\angle ALM сделаем вывод о том, что треугольник равнобедренный: AL=AM.
5. Найдём отношение AB:AL.
Решение.
1. Так как MK и AB лежат в плоскости ABD, то они пересекутся, L — точка их пересечения.
2. В \triangle MDK,\, \angle MDK=60^{\circ}, MD=2DK, значит, MK \perp BD. Действительно, допустим, что это не так. Тогда опустим перпендикуляр MK', MK' \perp BD. В прямоугольном треугольнике MK'D по определению косинуса \frac{K'D}{MD}=\cos \angle MDK', K'D=MD \cos 60^{\circ}=\frac12MD. Но тогда точки K и K' совпадают. Получили противоречие. Значит, MK \perp BD.
3. Обозначим AB=AD=a, тогда MD =\frac23a, DK =\frac13a, AM=\frac13a.
4. \angle DMK=30^{\circ}. Следовательно, \angle AML=30^{\circ} (по свойству вертикальных углов). Так как \angle MLA= 180^{\circ}-\angle MAL-\angle AML= 180^{\circ}-120^{\circ}-30^{\circ}= 30^{\circ}, то \triangle AML — равнобедренный и AL=AM=\frac13a.
5. Тогда AB:AL=a:\frac13a=3.
Замечание. Вместо рассуждений, проведённых в пункте 4, можно было рассмотреть прямоугольный треугольник LBK и воспользоваться свойством катета, лежащего против угла в 30^{\circ}.
б) План решения.
1. Угол между прямой и плоскостью — это угол между прямой и её проекцией на плоскость. Построим проекцию отрезка KL на плоскость ABC. Для этого опустим перпендикуляр KH, KH \perp ABC, точка H лежит в плоскости ABC. HL — проекция KL.
2. Найдём \sin \angle KLH (из треугольника KHL) и по синусу угла определим угол. Для этого выполним следующие действия.
2.1. Пусть O — центр основания ABC тетраэдра. Из подобия треугольников KHB и DOB найдём KH (для этого найдём DO).
2.2. Из треугольника BKL найдём KL.
2.3. Из треугольника KHL найдём \sin \angle KLH и \angle KLH.
Решение.
1. Искомый угол равен углу KLH.
2. Найдём \sin \angle KLH =\frac{KH}{KL}
2.1. \triangle KHB \sim \triangle DOB. Следовательно,
KH= \frac23DO= \frac23\sqrt {BD^2-BO^2}= \frac23\sqrt{BD^2-\left(\frac23BF\right)^2}= \frac23\sqrt {a^2-\left( \frac23\cdot \left( \frac{a\sqrt 3}2\right) \right) ^2}= \frac{2\sqrt 2}{3\sqrt 3}\cdot a.
2.2. В прямоугольном треугольнике BKL,\, BL =\frac43a, BK=\frac23a найдём KL=\sqrt {BL^2-BK^2} =\frac{2\sqrt 3}3a.
2.3. \sin \angle KLH =\frac{KH}{KL}=\frac{\sqrt 2}{3}, \angle KLH=arcsin \frac{\sqrt 2}3.
arcsin \frac{\sqrt 2}3.
Основанием четырехугольной пирамиды SABCD является прямоугольник со сторонами AB=12,BC=5. Боковые ребра SA= 3\sqrt{3},SB= \sqrt{171}, SD = 2\sqrt{13}.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между SC и BD.
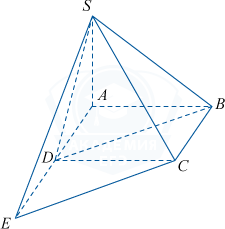
а) Заметим, что треугольник SAB является прямоугольным, так как в нем SB^2=171=27+144=SA^2+AB^2. Аналогично треугольник SAD тоже является прямоугольным, поскольку SD^2=52=27+25=SA^2+AD^2. Получаем, что прямая SA перпендикулярна прямым AB и AD, а значит, перпендикулярна плоскости основания ABCD.
б) Отложим на прямой AD за точку D отрезок DE, равный отрезку AD. Тогда в четырехугольнике BCED стороны BC и DE равны и параллельны. Следовательно, BCED является параллелограммом, поэтому BD\parallel CE, и угол между SC и BD будет равен углу между SC и CE.
По теореме Пифагора BD^2=AB^2+AD^2=144+25=169,
SC^2= SA^2+AC^2= SA^2+BD^2= 27+169= 196,
SE^2=SA^2+AE^2=27+100=127.
Значит, BD=CE=13, SC=14, SE=\sqrt{127}.
Пусть \angle SCE=\alpha. По теореме косинусов для треугольника SCE имеем: SE^2=SC^2+CE^2-2SC\cdot CE\cdot \cos \alpha,
\cos \alpha= \frac{SC^2+CE^2-SE^2}{2SC\cdot CE}= \frac{196+169-127}{2\cdot 13\cdot 14}= \frac{119}{182}.
Откуда \alpha=\arccos\frac{119}{182}.
б) \arccos\frac{119}{182}.
Площадь сечения, плоскостью SAC, правильной четырехугольной пирамиды SABCD равна 32\sqrt{3}, а площадь основания пирамиды ABCD равна 64.
а) Докажите, что угол между плоскостью основания, правильной четырехугольной пирамиды и боковым ребром равен 60^{\circ}.
б) Найдите площадь боковой поверхности пирамиды.
Сторона основания пирамиды равна 8. Тогда диагональ основания AC равна 8\sqrt{2}.
Пусть SH – высота пирамиды, тогда угол между боковым ребром SA и плоскостью основания – это угол SAC.
а) Площадь треугольника SAC равна \frac{1}{2}AC\cdot SH=32\sqrt{3}, откуда SH=\frac{64\sqrt{3}}{8\sqrt{2}}=4\sqrt{6}.
Следовательно, tg SAC=\frac{SH}{AH}= \frac{4\sqrt{6}}{4\sqrt{2}}=\sqrt{3}, а значит угол SAC равен 60^{\circ}.
б) Возьмем SM – за высоту грани SAB. Тогда получим
SM=\sqrt{SH^{2}+HM^{2}}=\sqrt{96+16}=4\sqrt{7}.
Отсюда следует S_{SAB}=\frac{SM\cdot AB}{2}=4\sqrt{7}\cdot 4=16\sqrt{7}.
Следовательно, площадь боковой поверхности равна 16\sqrt{7}\cdot 4=64\sqrt{7} – что и требовалось найти по условию.
б) 64\sqrt{7}
Закажите обратный звонок!