Задание №191
Условие
Основанием четырехугольной пирамиды SABCD является прямоугольник со сторонами AB=12,BC=5. Боковые ребра SA= 3\sqrt{3},SB= \sqrt{171}, SD = 2\sqrt{13}.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между SC и BD.
Решение
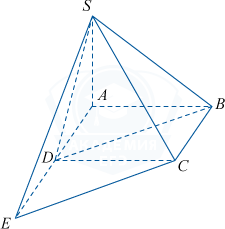
а) Заметим, что треугольник SAB является прямоугольным, так как в нем SB^2=171=27+144=SA^2+AB^2. Аналогично треугольник SAD тоже является прямоугольным, поскольку SD^2=52=27+25=SA^2+AD^2. Получаем, что прямая SA перпендикулярна прямым AB и AD, а значит, перпендикулярна плоскости основания ABCD.
б) Отложим на прямой AD за точку D отрезок DE, равный отрезку AD. Тогда в четырехугольнике BCED стороны BC и DE равны и параллельны. Следовательно, BCED является параллелограммом, поэтому BD\parallel CE, и угол между SC и BD будет равен углу между SC и CE.
По теореме Пифагора BD^2=AB^2+AD^2=144+25=169,
SC^2= SA^2+AC^2= SA^2+BD^2= 27+169= 196,
SE^2=SA^2+AE^2=27+100=127.
Значит, BD=CE=13, SC=14, SE=\sqrt{127}.
Пусть \angle SCE=\alpha. По теореме косинусов для треугольника SCE имеем: SE^2=SC^2+CE^2-2SC\cdot CE\cdot \cos \alpha,
\cos \alpha= \frac{SC^2+CE^2-SE^2}{2SC\cdot CE}= \frac{196+169-127}{2\cdot 13\cdot 14}= \frac{119}{182}.
Откуда \alpha=\arccos\frac{119}{182}.
Ответ
б) \arccos\frac{119}{182}.