Задания по теме «Расстояние между прямыми»

а) Рассмотрим рисунок.

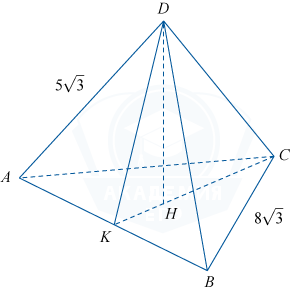
Так как все боковые рёбра наклонены под одним и тем же углом к основанию, то основание высоты пирамиды (на рисунке это точка H ) является центром окружности, описанной около треугольника ABC. Но треугольник ABC — правильный, поэтому H является точкой пересечения высот (а значит, и медиан). Отсюда следует, что AB \perp CK.

По условию боковые рёбра пирамиды равны, поэтому треугольник ABD равнобедренный, DK является его медианой, значит, и высотой. Значит, AB \perp DK. Получаем, что AB перпендикулярна двум пересекающимся прямым, лежащим в плоскости KDC, поэтому AB \perp KDC.

Следовательно, AB \perp CD.

б) Проведем в треугольнике KDC высоту KT.

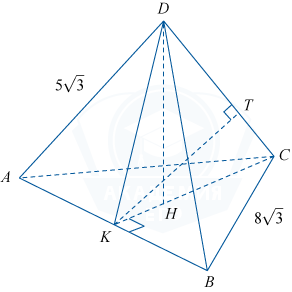
Так как AB \perp KDC, то AB \perp KT. Значит, KT является общим перпендикуляром к прямым AB и CD, а длина отрезка KT является расстоянием между прямыми AB и CD.

В равностороннем треугольнике ABC высота KC=AC\cdot \cos 30^{\circ}=8\sqrt 3\cdot \frac{\sqrt 3}2=12, KH=\frac12KC=4. В треугольнике ADK,\, AK=\frac12AB=4\sqrt 3,

KD= \sqrt {AD^2-AK^2} = \sqrt {\left( 5\sqrt 3\right) ^2-\left( 4\sqrt 3\right) ^2}= 3\sqrt 3.

В прямоугольном треугольнике DHK

DH= \sqrt {KD^2-KH^2}= \sqrt {27-16}= \sqrt {11}.

2\cdot S_{KDC}=KC\cdot DH=KT\cdot DC.

KT=\frac{KC\cdot DH}{DC}=\frac{12\cdot \sqrt {11}}{5\sqrt 3}=\frac{4\sqrt {33}}5.

\frac{4\sqrt {33}}5.

а) Ясно, что CC_{1} \perp A_{1}B_{1}C_{1}, так как ABCDA_{1}B_{1}C_{1}D_{1} — прямая призма.

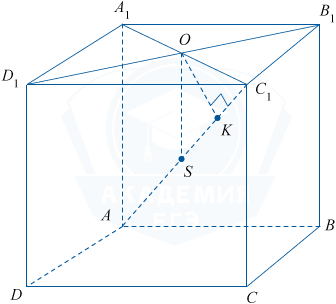
Тогда A_{1}C_{1} — проекция AC_{1} на плоскость A_{1}B_{1}C_{1}. При этом B_{1}D_{1} \perp A_{1}C_{1} по свойству диагоналей ромба. Тогда по теореме о трёх перпендикулярах B_{1}D_{1} \perp AC_{1}, что и требовалось доказать.

б) Пусть O — точка пересечения диагоналей ромба A_{1}C_{1} и B_{1}D_{1}. В плоскости AA_{1}C_{1} проведем OK \perp AC_{1}, где точка K принадлежит AC_{1}. Но A_{1}C_{1} \perp B_{1}D_{1}, B_{1}D_{1} \perp AC_{1}, следовательно, B_{1}D_{1} \perp AA_{1}C_{1} по признаку перпендикулярности прямой и плоскости. Тогда B_{1}D_{1} перпендикулярна любой прямой в плоскости (AA_{1}C_{1}).

В частности, B_{1}D_{1} \perp OK. Значит, длина отрезка OK равна расстоянию между скрещивающимися прямыми AC_{1} и B_{1}D_{1}.

В треугольнике AA_{1}C_{1} проведём среднюю линию OS. Тогда OS=\frac{1}{2}AA_{1}=10 и OS \parallel AA_{1}, значит, OS \perp A_{1}C_{1} и \bigtriangleup OSC_{1} — прямоугольный. C_{1}O=\frac{1}{2}A_{1}C_{1}=5, S_{SOC_{1}}=\frac{1}{2}SO \cdot OC_{1}=\frac{1}{2}C_{1}S \cdot OK. Отсюда OK= \frac{C_{1}O \cdot OS}{C_{1}S}= \frac{5 \cdot 10}{\sqrt{5^2+10^2}}= \frac{50}{5\sqrt{5}}= 2\sqrt{5}.

2\sqrt{5}.

а) Прямая MN лежит в плоскости \left (MNN_{1} \right ), \left (M_{1}P_{1} \right ) и пересекает \left (MNN_{1} \right ) в точке M_{1}, тогда по признаку скрещивающихся прямых MN и M_{1}P_{1} — скрещивающиеся прямые.

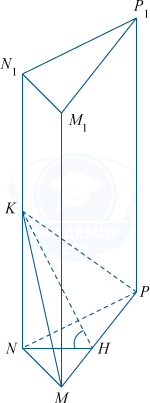
Плоскости MNP и M_{1}N_{1}P_{1} параллельны как основания призмы. По условию, призма прямая, значит, каждое боковое ребро перпендикулярно основаниям, следовательно, является расстоянием между скрещивающимися прямыми MN и M_{1}P_{1}, что и требовалось доказать.

б) Проведем NH\perp MP, тогда NH — высота и медиана в равнобедренном \bigtriangleup MNP. KH — медиана \bigtriangleup MKP. NH — проекция KH на \left (MPN \right ) и NH\perp MP. Следовательно, KH\perp MP (по теореме о трех перпендикулярах).

\angle KHN — линейный угол двугранного угла KMPN, откуда \angle KHN = 60^{\circ}.

В \bigtriangleup KPH катет KH=\sqrt{KP^{2}-PH^{2}}= \sqrt{81-27}=\sqrt{54}=3\sqrt{6}.

Из \bigtriangleup KNH катет KN = KH \cdot \sin 60^{\circ} = 3 \sqrt{6} \cdot \frac{\sqrt{3}}{2} = \frac{9\sqrt{2}}{2}.

По условию NK : N_{1}K = 3:4, N_{1}K= \frac{4}{3}NK, N_{1}K=6\sqrt{2}.

NN_{1}=NK+N_{1}K=\frac{21\sqrt{2}}{2}.

\frac{21\sqrt{2}}{2}