Задание №190
Условие
Треугольник MNP со сторонами MP=6\sqrt{3} и MN=NP лежит в основании прямой призмы MNPM_{1}N_{1}P_{1}. Точка K выбрана на ребре NN_{1} таким образом, что NK:N_{1}K=3:4. При этом угол между плоскостью MNP и плоскостью MKP составляет 60^{\circ}.
а) Докажите, что расстояние между прямыми MN и M_1P_1 равно боковому ребру призмы.
б) При условии KP=9, вычислите расстояние между прямыми MN и M_{1}P_{1}.
Решение
а) Прямая MN лежит в плоскости \left (MNN_{1} \right ), \left (M_{1}P_{1} \right ) и пересекает \left (MNN_{1} \right ) в точке M_{1}, тогда по признаку скрещивающихся прямых MN и M_{1}P_{1} — скрещивающиеся прямые.
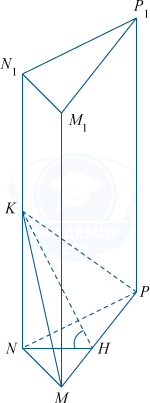
Плоскости MNP и M_{1}N_{1}P_{1} параллельны как основания призмы. По условию, призма прямая, значит, каждое боковое ребро перпендикулярно основаниям, следовательно, является расстоянием между скрещивающимися прямыми MN и M_{1}P_{1}, что и требовалось доказать.
б) Проведем NH\perp MP, тогда NH — высота и медиана в равнобедренном \bigtriangleup MNP. KH — медиана \bigtriangleup MKP. NH — проекция KH на \left (MPN \right ) и NH\perp MP. Следовательно, KH\perp MP (по теореме о трех перпендикулярах).
\angle KHN — линейный угол двугранного угла KMPN, откуда \angle KHN = 60^{\circ}.
В \bigtriangleup KPH катет KH=\sqrt{KP^{2}-PH^{2}}= \sqrt{81-27}=\sqrt{54}=3\sqrt{6}.
Из \bigtriangleup KNH катет KN = KH \cdot \sin 60^{\circ} = 3 \sqrt{6} \cdot \frac{\sqrt{3}}{2} = \frac{9\sqrt{2}}{2}.
По условию NK : N_{1}K = 3:4, N_{1}K= \frac{4}{3}NK, N_{1}K=6\sqrt{2}.
NN_{1}=NK+N_{1}K=\frac{21\sqrt{2}}{2}.
Ответ
\frac{21\sqrt{2}}{2}