Задания по теме «Объем тела»

а) 1. Построим сечение призмы плоскостью \gamma.

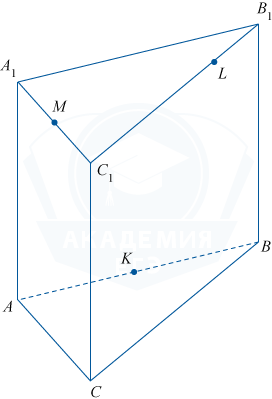
Плоскость ABC проходит через прямую AC, параллельную плоскости \gamma, и пересекает её (K — общая точка этих плоскостей), следовательно, линия пересечения этих плоскостей параллельна прямой AC. В плоскости ABC построим среднюю линию KN. Аналогично в плоскости A_1B_1C_1 проведём LF \parallel A_1C_1. FKNL — сечение призмы плоскостью \gamma.

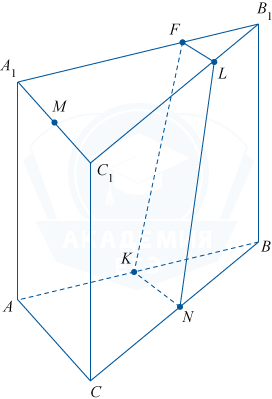
2. Докажем, что BM \perp \gamma.

Проведём MT \parallel AA_1. Плоскость BTM перпендикулярна прямой AC. Действительно, AC перпендикулярна двум пересекающимся прямым (MT, BT) плоскости BTM. Следовательно, BM \perp AC, значит, BM \perp KN.

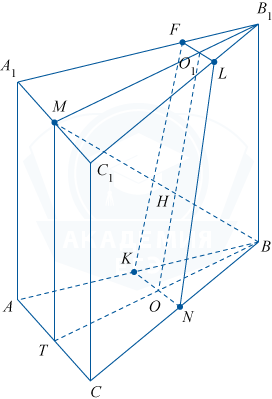
Докажем теперь, что MB \perp OO_1. Рассмотрим прямоугольник BTMB_1.

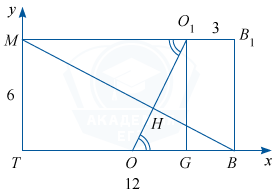
MT=6, B_1O_1=3, BT=12 (высоты правильных треугольников B_1FL и ABC соответственно). Введём систему координат и найдём скалярное произведение векторов \overline{MB} и \overline{OO_1}.

M(0; 6), B(12; 0), \overline{MB}\{12; -6\}, O(6; 0), O_1(9; 6) , \overline{OO_1}\{3; 6\}.

\overline{MB}\cdot \overline{OO_1}=12\cdot 3+(-6)\cdot 6=0. Это означает, что векторы \overline{MB} и \overline{OO_1} перпендикулярны, следовательно, MB \perp OO_1. Итак, MB перпендикулярна двум пересекающимся прямым KN и OO_1 плоскости \gamma , а значит, MB\perp \gamma.

б) \triangle MHO_1 \sim \triangle OO_1G как прямоугольные треугольники с равными острыми углами, \angle MO_1H=\angle GOO_1 как накрест лежащие при MB_1 \parallel BT и секущей OO_1. Из этого следует, что \frac{MO_1}{OO_1}=\frac{MH}{O_1G}, MO_1=9, O_1G=6, OO_1 найдём по теореме Пифагора из прямоугольного треугольника OO_1G. OO_1= \sqrt {OG^2+O_1G^2}= \sqrt {9+36}= \sqrt {45}=3\sqrt5. 9\cdot 6=3\sqrt 5MH, откуда MH =\frac{18\sqrt 5}5. MH — высота пирамиды MKNLF.

Площадь равнобедренной трапеции KNLF с основаниями KN и LF и высотой OO_1 равна \frac{KN+LF}2\cdot OO_1. KN — средняя линия треугольника ABC, KN=\frac12AB=4\sqrt 3. LF — сторона правильного треугольника LB_1F (LF \parallel A_1C_1), поэтому LF= LB_1= 2\sqrt 3. S_{KNLF}= \frac{4\sqrt 3+2\sqrt 3}{2}\cdot 3\sqrt 5= 9\sqrt {15}.

V_{MKNLF} = \frac13S_{KNLF}\cdot MH= \frac13\cdot 9\sqrt {15}\cdot \frac{18\sqrt 5}5= 54\sqrt 3.

54\sqrt 3.

Построим сначала сечение пирамиды плоскостью \gamma.

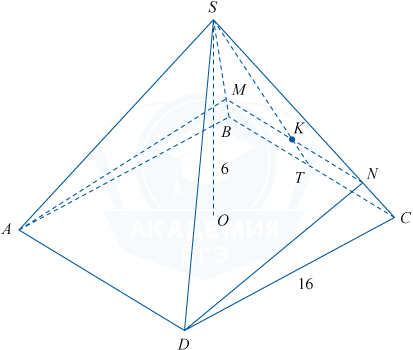
а) Плоскость \gamma пересекает плоскость SAD по прямой AD, а плоскость SBC — по прямой MN, проходящей через точку K, параллельной BC (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения параллельна этой прямой). ADNM — сечение пирамиды плоскостью \gamma. ADNM — равнобедренная трапеция.

BC \parallel \gamma, следовательно, все точки, принадлежащие прямой BC, равноудалены от плоскости \gamma. Значит, расстояние от точки B до плоскости \gamma равно расстоянию от точки C до плоскости \gamma. Что и требовалось доказать.

б) Так как расстояние от любой точки прямой BC до плоскости \gamma одно и то же, будем искать расстояние от точки T до плоскости \gamma, то есть нужно из точки T провести отрезок TH, перпендикулярный плоскости ADN, который равен высоте пирамиды BADNM. Тогда V_{BADNM}=\frac{1}{3}S_{ADNM} \cdot TH.

K — середина отрезка MN, так как принадлежит апофеме ST. Обозначим через P середину отрезка AD, тогда KP \perp AD как высота равнобедренной трапеции ADNM. S_{BADNM}=\frac{AD+MN}{2} \cdot PK.

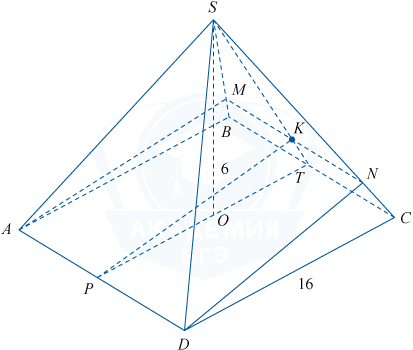
AD \perp PST, действительно, KP \perp AD и PT \perp AD, следовательно, достаточно построить отрезок TH \perp PK, так как тогда TH перпендикулярна двум пересекающимся прямым плоскости \gamma (AD и PK).

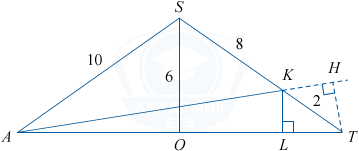
S_{\bigtriangleup PKT} выразим двумя способами:

\frac{1}{2} TH \cdot PK=\frac{1}{2} PT \cdot KL, откуда TH=\frac{PT \cdot KL}{PK}.

Из прямоугольного треугольника SOT с катетами OT=8, SO=6 и гипотенузой ST по теореме Пифагора ST=10, находим KL из подобия прямоугольных треугольников SOT и KLT с общим острым углом STO:

\frac{SO}{KL}=\frac{ST}{KT}=\frac{OT}{LT}, \frac{6}{KL}=\frac{10}{2}, KL=\frac{6}{5}. Далее \frac{8}{LT}=\frac{10}{2}, LT=\frac{8}{5}, OL=OT-LT=8-\frac{8}{5}=\frac{32}{5}.

PK найдем по теореме Пифагора из прямоугольного треугольника PKL:

PK^{2}= PL^{2}+LK^{2}= (PO+OL)^{2}+LK^{2},

PK^{2}= \left ( 8+\frac{32}{5} \right )^{2}+\left ( \frac{6}{5}\right )^{2}= \frac{5220}{25} \cdot PK= \frac{6\sqrt{145}}{5}.

TH=\frac{PT \cdot KL}{PK}=\frac{16 \cdot \dfrac{6}{5}}{\dfrac{6\sqrt{145}}{5}}=\frac{16}{\sqrt{145}}.

Основание MN равнобедренной трапеции найдем из подобия треугольников SMN и SBC, высоты которых SK=8, ST=10.

\frac{MN}{BC}=\frac{SK}{ST}, \frac{MN}{16}=\frac{8}{10}, откуда MN=\frac{64}{5}.

V_{BADNM}= \frac{1}{3} \cdot \frac {AD+MN}{2} \cdot PK \cdot TH= \frac{1}{3} \cdot \frac{16+\dfrac{64}{5}}{2} \cdot \frac{6\sqrt{145}}{5} \cdot \frac{16}{\sqrt{145}}= 92,16.

92,16

а) На основании условия рассмотрим чертеж, где SO — высота пирамиды, PT — средняя линия треугольника ABD, E — середина SO, \angle SAC=45^{\circ}, O_{1} — середина AO.

PT\parallel BD (как средняя линия \bigtriangleup ABD), поэтому PT\parallel SBD. Значит, \alpha пересекает плоскость SBD по прямой параллельной PT (а значит, и BD), проходящей через точку E.

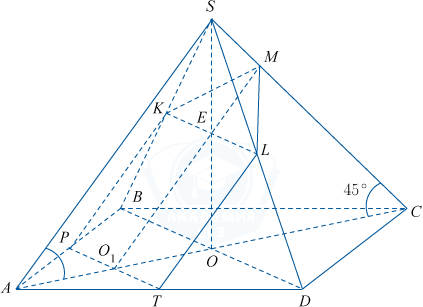
Обозначим точки пересечения этой прямой с ребрами SB и SD через K и L соответственно.

Точки O_{1} и E лежат в плоскости \alpha, значит, прямая O_{1}E также лежит в этой плоскости. Обозначим через M точку пересечения этой прямой с ребром SC. Соединяя последовательно точки T, P, K, M, L и T, получим искомое сечение.

DB\perp ASC, так как DB\perp OS и DB\perp OA. LK\parallel BD, согласно вышесказанному, поэтому LK\perp ASC. Отсюда следует, что LK\perp SM.

O_{1}E \parallel AS (O_{1}E — средняя линия \bigtriangleup ASO), AS \perp SC, так как \angle ASC=90^{\circ}, поэтому O_{1}E \perp SC. Отсюда следует, что \alpha \perp SC, (\alpha проходит через пересекающиеся прямые LK и O_{1}E, перпендикулярные SC).

б) Из доказанного выше утверждения следует, что SM является высотой пирамиды SKLM и KL\perp EM.

Так как \angle ESM=45^{\circ} и \bigtriangleup SME — прямоугольный, то SM=ME.

V_{SKLM}= \frac{1}{3}S_{KLM} \cdot SM = \frac{1}{3} \cdot \frac{1}{2}KL \cdot EM \cdot SM = \frac{1}{6}KL \cdot SM^{2}.

\bigtriangleup ASC \sim \bigtriangleup O_{1}MC, \: AO_{1} = \frac{1}{4} AC, поэтому SM=\frac{1}{4}SC.

Заметим, что треугольники ASC и ADC равны (по стороне и двум прилежащим углам), поэтому SC=CD=4 и SM=\frac{1}{4} \cdot 4=1.

Наконец, KL=\frac{1}{2}BD=\frac{1}{2}\cdot 4\sqrt{2}=2\sqrt{2}. Отсюда получаем:

V_{SKLM}=\frac{1}{6}\cdot 2\sqrt{2} \cdot 1^{2}=\frac{\sqrt{2}}{3}.

\frac{\sqrt{2}}{3}