Задание №185
Условие
В правильной четырехугольной пирамиде SABCD с диагональю основания BD и вершиной S, боковое ребро образует угол 45^{\circ} с основанием, при этом, сторона основания равна 4.
Плоскость \alpha проведена через среднюю линию треугольника ABD, не пересекающую середину высоты пирамиды и BD.
а) Постройте сечение пирамиды плоскостью \alpha и докажите, что ребро SC и плоскость \alpha перпендикулярны.
б) K, L, M — точки пересечения ребер SC, SD, SB с плоскостью \alpha. Найдите объем пирамиды SKLM.
Решение
а) На основании условия рассмотрим чертеж, где SO — высота пирамиды, PT — средняя линия треугольника ABD, E — середина SO, \angle SAC=45^{\circ}, O_{1} — середина AO.
PT\parallel BD (как средняя линия \bigtriangleup ABD), поэтому PT\parallel SBD. Значит, \alpha пересекает плоскость SBD по прямой параллельной PT (а значит, и BD), проходящей через точку E.
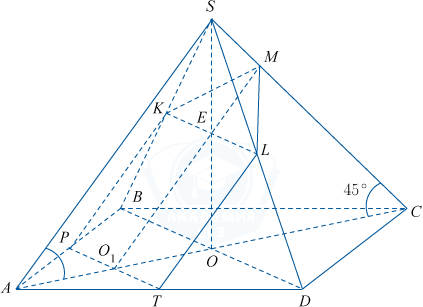
Обозначим точки пересечения этой прямой с ребрами SB и SD через K и L соответственно.
Точки O_{1} и E лежат в плоскости \alpha, значит, прямая O_{1}E также лежит в этой плоскости. Обозначим через M точку пересечения этой прямой с ребром SC. Соединяя последовательно точки T, P, K, M, L и T, получим искомое сечение.
DB\perp ASC, так как DB\perp OS и DB\perp OA. LK\parallel BD, согласно вышесказанному, поэтому LK\perp ASC. Отсюда следует, что LK\perp SM.
O_{1}E \parallel AS (O_{1}E — средняя линия \bigtriangleup ASO), AS \perp SC, так как \angle ASC=90^{\circ}, поэтому O_{1}E \perp SC. Отсюда следует, что \alpha \perp SC, (\alpha проходит через пересекающиеся прямые LK и O_{1}E, перпендикулярные SC).
б) Из доказанного выше утверждения следует, что SM является высотой пирамиды SKLM и KL\perp EM.
Так как \angle ESM=45^{\circ} и \bigtriangleup SME — прямоугольный, то SM=ME.
V_{SKLM}= \frac{1}{3}S_{KLM} \cdot SM = \frac{1}{3} \cdot \frac{1}{2}KL \cdot EM \cdot SM = \frac{1}{6}KL \cdot SM^{2}.
\bigtriangleup ASC \sim \bigtriangleup O_{1}MC, \: AO_{1} = \frac{1}{4} AC, поэтому SM=\frac{1}{4}SC.
Заметим, что треугольники ASC и ADC равны (по стороне и двум прилежащим углам), поэтому SC=CD=4 и SM=\frac{1}{4} \cdot 4=1.
Наконец, KL=\frac{1}{2}BD=\frac{1}{2}\cdot 4\sqrt{2}=2\sqrt{2}. Отсюда получаем:
V_{SKLM}=\frac{1}{6}\cdot 2\sqrt{2} \cdot 1^{2}=\frac{\sqrt{2}}{3}.
Ответ
\frac{\sqrt{2}}{3}