Задание №911
Условие
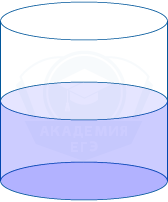
В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 15 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объём детали? Ответ выразите в см3.
Решение
Пусть R — радиус основания цилиндра, а h — уровень воды, налитой в сосуд. Тогда объём налитой воды равен объёму цилиндра с радиусом основания R и высотой h. Vводы = Sосн. · h = \pi R^2\cdot h. Согласно условию выполняется равенство 2000=\pi R^2\cdot15. Отсюда, \pi R^2=\frac{2000}{15}=\frac{400}{3}.
Пусть H — уровень воды в сосуде после погружения в него детали. Тогда суммарный объем воды и детали равен объему цилиндра с радиусом основания R и высотой H. По условию H=h+9=15+9=24. Значит, Vводы + детали = \pi R^2\cdot H=\frac{400}{3}\cdot24=3200. Следовательно, Vдетали = Vводы + детали − Vводы = 3200-2000=1200.