Задание №269
Условие
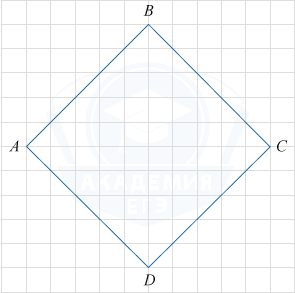
Найдите радиус окружности, вписанной в квадрат ABCD, если стороны квадратных клеток равны \frac{\sqrt2}{2}.
Решение
Диаметр окружности, вписанной в квадрат, равен стороне квадрата.
Из рисунка, на котором в условии задачи изображен квадрат, делаем вывод, что сторона квадрата равна 5-ти диагоналям квадрата со стороной \frac{\sqrt2}{2}.
По теореме Пифагора d= \sqrt{ \left ( \frac{\sqrt2}{2} \right )^2 + \left ( \frac{\sqrt2}{2} \right )^2 } = \sqrt{\frac12+\frac12}= 1.
Значит, сторона квадрата равна 5, а радиус окружности равен 2,5.
Ответ
2,5
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.