Задание №207
Условие
Найдите все значения параметра a, при каждом из которых неравенство
x^2+3|x-a|-7x\leqslant -2a
имеет единственное решение.
Решение
Неравенство равносильно совокупности систем неравенств
\left[\!\!\begin{array}{l} \begin{cases} x \geqslant a, \\ x^2+3x-3a-7x+2a\leqslant0; \end{cases} \\ \begin{cases}x<a, \\ x^2-3x+3a-7x+2a\leqslant0. \end{cases}\end{array}\right. \left[\!\!\begin{array}{l} \begin{cases} x \geqslant a, \\ x^2-4x-a\leqslant0; \end{cases} \\ \begin{cases}x<a, \\ x^2-10x+5a\leqslant0; \end{cases}\end{array}\right. \left[\!\!\begin{array}{l} \begin{cases} a \leqslant x, \\ a\geqslant x^2-4x; \end{cases} \\ \begin{cases}a>x, \\ a\leqslant -\frac{x^2}{5}+2x. \end{cases}\end{array}\right.
В системе координат Oxa построим графики функций a=x, a=x^2-4x, a=-\frac{x^2}{5}+2x.
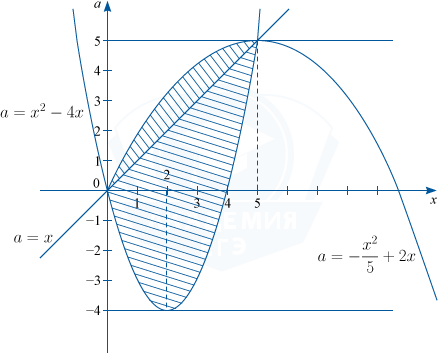
Полученной совокупности удовлетворяют точки, заключенные между графиками функций a=x^2-4x, a=-\frac{x^2}{5}+2x на промежутке x\in [0;5] (заштрихованная область).
По графику определяем: исходное неравенство имеет единственное решение при a=-4 и a=5, так как в заштрихованной области будет единственная точка с ординатой a, равной -4 и равной 5.
Ответ
-4; 5