Задание №195

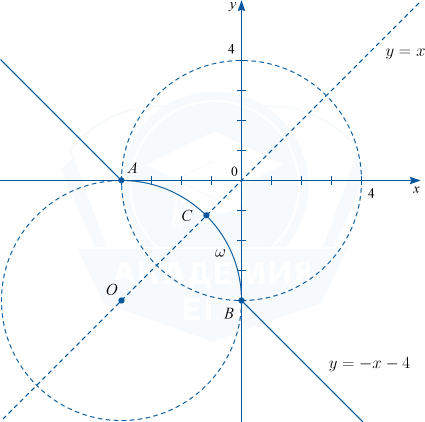
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.

Рассмотрим два случая:

1) Если x^2+y^2 \geqslant 16, получаем уравнение

x^2+16x+y^2+16y+48=x^2+y^2-16

16x+16y=-64

y=-x-4

Это уравнение при соответствующих значениях x и y, удовлетворяющих неравенству x^2+y^2 \geqslant 16, задает два луча, выходящих из точек A(-4; 0) и B(0; -4) и расположенных на прямой y=-x-4.

2) Если x^2+y^2 < 16, то получаем уравнение

x^2+16x+y^2+16y+48=16-x^2-y^2

2x^2+16x+2y^2+16y+32=0

(x+4)^2+(y+4)^2=4^2

Это уравнение при соответствующих значениях x и y, удовлетворяющих неравенству x^2+y^2< 16, задает дугу \omega окружности с центром в точке O(-4;-4) и радиусом 4 с концами в точках A и B.

Рассмотрим второе уравнение системы. Оно задает прямую y=-x+a, параллельную прямой АВ или совпадающую с ней при a= -4 (в этом случае система имеет бесконечное множество решений).

Очевидно, что при a< -4 система решений иметь не будет.

При a> -4 система уравнений будет иметь более одного решения тогда и только тогда, когда прямая y=-x+a будет пересекать дугу \omega в двух различных точках.

Найдем, при каком значении a прямая y=-x+a касается дуги \omega. Из соображений симметрии заметим, что касание происходит в точке С с координатами (x_0; y_0), которая находится на прямой y=x, откуда x_0 = y_0. Подставляя координаты точки C(x_0; x_0) в уравнение, которое задает дугу \omega, имеем:

(x_0+4)^2+(x_0+4)^2=4^2

|x_0+4|=2\sqrt{2}

x_0=2\sqrt{2}-4; x_0=-2\sqrt{2} -4 не принадлежит дуге \omega.

Тогда a=x_0+y_0=2x_0=4\sqrt{2}-8.

Значит, при -4 < a <4\sqrt{2}-8 система имеет два решения, при a = 4\sqrt{2}-8 система имеет одно решение, при a >4\sqrt{2}-8 система решений не имеет.

[-4; 4\sqrt{2}-8)