Задание №161

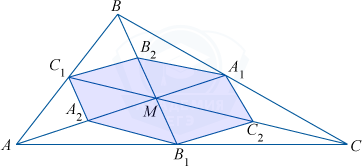а) Площадь треугольника C_{1}MB_{2} в два раза меньше площади треугольника C_{1}MB, так как MB=2MB_{2}, а высота C_{1} у этих треугольников одна и та же. S_{C_{1}MB}=2S_{C_{1}MB_{2}}

Исходя из этого получаем равенства:

S_{A_{1}MB}=2S_{A_{1}MB_{2}}, S_{A_{1}MC}=2S_{A_{1}MC_{2}}, S_{B_{1}MC}=2S_{B_{1}MC_{2}}, S_{B_{1}MA}=2S_{B_{1}MA_{2}}, S_{C_{1}MA}=2S_{C_{1}MA_{2}}

Складывая почленно получаем: S_{ABC}=2S_{A_{1}C_{2}B_{1}A_{2}C_{1}B_{2}}

б) Обозначим длины сторон BC, AC, AB треугольника ABC буквами a, b, c.

Докажем, что квадрат медианы AA_{1} равен \frac{1}{4}\left ( 2b^{2}+2c^{2}-a^{2} \right ).

Для доказательства на продолжении отрезка AA_{1} за точку A_{1} отложим отрезок A_{1}P=AA_{1}. Получим параллелограмм ACPB со сторонами AC = PB = b, AB = CP = c, и диагоналям BC = a и AP = 2AA_{1}. Сумма квадратов диагоналей равна сумме квадратов его сторон:

2b^{2}+2c^{2}=a^{2}+4AA_{1}^{2}, откуда AA_{1}^{2}=\frac{1}{4}(2b^{2}+2c^{2}-a^{2}).

Аналогично доказывается, что BB_{1}^{2}=\frac{1}{4}(2a^{2}+2c^{2}-b^{2}), а CC_{1}^{2}=\frac{1}{4}(2a^{2}+2b^{2}-c^{2}).

Отрезок C_{1}A_{2} – средняя линия треугольника ABM, значит,

C_{1}A_{2}=\frac{1}{2}BM=\frac{1}{2}\cdot \frac{2}{3}BB_{1}=\frac{1}{3}BB_{1}.

Рассуждая аналогично, мы получим, что стороны шестиугольника втрое меньше медиан треугольника ABC:

B_{2}C_{1}=B_{1}C_{2}= \frac{1}{3}AA_{1}, A_{2}B_{1}= A_{1}B_{2}=\frac{1}{3}CC_{1}. Следовательно, сумма квадратов сторон шестиугольника равна:

2\cdot (B_{1}C_{2}^{2}+A_{1}C_{2}^{2}+A_{1}B_{2}^{2})= \frac{2}{9}(AA_{1}^{2}+BB_{1}^{2}+CC_{1}^{2})= \frac{2}{9}\cdot \frac{1}{4}\cdot (2b^{2}+2c^{2}-a^{2}+2a^{2}+2c^{2}-b^{2}+2a^{2}+2b^{2}-c^{2})= \frac{1}{18}\cdot 3\cdot (a^{2}+b^{2}+c^{2})= \frac{1}{6}\cdot (a^{2}+b^{2}+c^{2}).

Подставляя в эту формулу длины сторон треугольника ABC, получаем ответ: сумма квадратов сторон шестиугольника равна \frac{63}{2}.

б) \frac{63}{2}