Задание №188

Тип задания: 16
Тема: Задачи на доказательство

Условие

В треугольнике ABC окружность проходит через точки B и C и пересекает стороны AB и AC в точках M и N соответственно. Отрезок MN касается окружности, вписанной в треугольник ABC.

а) Докажите, что \bigtriangleup ABC подобен \bigtriangleup ANM.

б) Найдите MN, если AB=7, AC=8, BC=9.

Показать решение

Решение

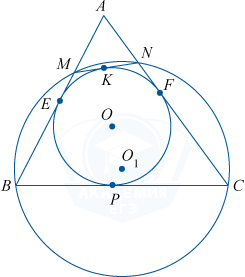
Окружность вписанная в треугольник ABC и окружность проходящая через точки B и C

а) Окружность с центром в точке O_1 описана около четырехугольника BMNC, значит, \angle BCN+\angle BMN =180^{\circ}, \angle BMN=180^{\circ}-\angle BCN. \angle AMN+\angle BMN=180^{\circ}, как смежные, \angle BMN=180^{\circ}-\angle AMN.

Отсюда \angle BCN=\angle AMN.

Имеем в треугольниках ABC и ANM: \angle A - общий, \angle ACB=\angle NCB=\angle AMN, значит, \bigtriangleup ABC подобен \bigtriangleup ANM по первому признаку подобия, что требовалось доказать.

б) Из подобия следует \frac{AB}{AN}=\frac{AC}{AM}=\frac{BC}{MN}.

Окружность с центром в точке O вписана в \bigtriangleup ABC, значит

AF=AE, BE=BP, CP=CF, как отрезки касательных, проведенных к окружности c центром O_1 из точек A, B и C соответственно.

Пусть AF=AE=x, тогда BE=BP=7-x, CP=CF=8-x, BP+CP=BC, 7-x+8-x=9, x=3, AF=AE=3.

Обозначим MK=t, NK=p, тогда ME=MK=t, NF=NK=p как отрезки касательных, проведенных к окружности с центром O из точек M и N соответственно.

Получим AM=AE-ME=3-t, AN=AF-NF=3-p, MN=MK+NK=t+p.

Периметр \bigtriangleup AMN равен AM+AN+MN=3-t+3-p+t+p=6.

Периметры подобных треугольников относятся так же как и их стороны, поэтому \frac{6}{7+8+9}=\frac{MN}{9}, MN=\frac{54}{24}=2,25