Задание №158
Условие
а) Решите уравнение 2\sin ^{4}x+3\cos 2x+1=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку \left [\pi;3\pi \right ]
Решение
а) Воспользуемся формулой \sin ^{2}x=\frac{1-\cos 2x}{2}.
Из нее следует, что \sin ^{4}x=\frac{1}{4}\left ( \cos ^{2}2x-2\cos 2x+1 \right ).
Поэтому уравнение можно преобразовать так:
\frac{1}{2}\cos ^{2}2x-\cos 2x+\frac{1}{2}+3\cos 2x+1=0
\cos ^{2}2x+4\cos 2x+3=0
Сделаем замену t=\cos 2x:
t^{2}+4t+3=0
t=-1 или t=-3
Сделаем обратную замену:
\cos 2x=-1 или \cos 2x=-3.
Уравнение \cos 2x=-3 не имеет решений. Из уравнения \cos 2x=-1 получаем
2x=\pi +2\pi n, n\in \mathbb{Z}
x=\frac{\pi }{2}+\pi n, n\in \mathbb{Z}
б) При помощи тригонометрической окружности отберем корни, принадлежащие заданному отрезку.
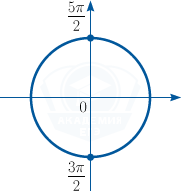
Получим x=\frac{3\pi }{2}, x=\frac{5\pi }{2}.
Ответ
а) \frac{\pi }{2}+\pi n, n\in \mathbb{Z}; б) \frac{3\pi }{2}; \frac{5\pi}{2}.
Бунёд Хидоятов /
Бунёд Хидоятов /
Инна Бирюкова /
Дмитрий Елисеев /
Задания с 13 по 19 имеют развернутый ответ. При прохождении тестирования решения этих заданий и ответы нужно вручную сверять с решениями и ответами на сайте. Это делается на этапе подведения итогов. Поэтому ответы для этих заданий можно не вписывать в текстовую область, а записать, например, у себя в тетради и уже потом свериться.