Задание №1014

Заметим, что при a < 0 неравенство системы не имеет решения, потому что левая часть неравенства неотрицательна. При a=0 оно имеет вид x^{2}+y^{2} \leq 0 и имеет единственное решение x=y=0.

Рассмотрим a > 0. Решим задачу, построив графики уравнения и неравенства. Графиком неравенства системы будет являться круг радиусом \sqrt{a} с центром в точке (\sin \pi a;a).

Графиком уравнения будут стороны угла.

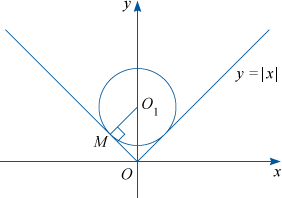
Ровно два решения будет, если круг касается обеих сторон угла, тогда центр круга должен лежать на биссектрисе угла, то есть на луче Oy. Значит, абсцисса центра круга должна равняться нулю, \sin \pi a=0, \pi a=\pi k, k \in \mathbb Z, a=k. Значит, a \in \mathbb Z. Рассмотрим \bigtriangleup O_{1}MO, где O_{1} — центр круга, M — одна из точек касания. Тогда O_{1}O=a,  O_{1}M=\sqrt{a},  \angle O_{1}MO=90^\circ,  \angle O_{1}OM=45^\circ. Отсюда O_{1}M=O_{1}O \sin \angle O_{1}OM=\frac{a\sqrt{2}}{2}. Следовательно, \frac{a\sqrt{2}}{2}=\sqrt{a}, \sqrt{a}=\sqrt{2}, a=2. Ясно, что 2 \in \mathbb Z.

2