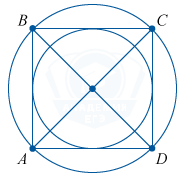
Квадрат
Квадрат — это четырехугольник, имеющий равные стороны и углы.
.png)
Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.
Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.
Свойства квадрата
1. Длины сторон квадрата равны.
AB=BC=CD=DA
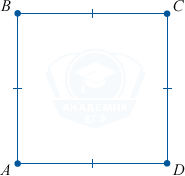
2. Все углы квадрата прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}
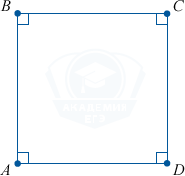
3. Противолежащие стороны квадрата параллельны друг другу.
AB \parallel CD, BC \parallel AD
4. Сумма всех углов квадрата равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}
5. Величина угла между диагональю и стороной равна 45 градусов.
\angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^{\circ}
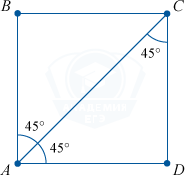
Доказательство
Квадрат является ромбом \Rightarrow AC — биссектриса угла A, и он равняется 45^{\circ}. Тогда AC делит \angle A, и \angle C на 2 угла по 45^{\circ}.
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
AO = BO = CO = DO
\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^{\circ}
AC = BD
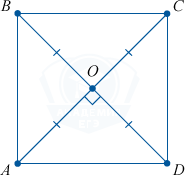
Доказательство
Так как квадрат это прямоугольник \Rightarrow диагонали равны; так как — ромб \Rightarrow диагонали перпендикулярны. А так как — параллелограмм, \Rightarrow диагонали разделены точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
\triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
\triangle AOB = \triangle BOC = \triangle COD = \triangle AOD
9. Если сторона квадрата равна a, то, диагональ будет равна a \sqrt{2}.
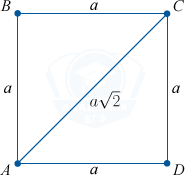
Доказательство
Доказывается по теореме Пифагора. Применим ее к \triangle ADC.
AC^{2} = AD^{2} + DC^{2} = a^{2} + a^{2} = 2^{2}
Отсюда: AC = \sqrt{2}\cdot a
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей