Ромб
Ромб — это четырехугольник, имеющий равные длины сторон.
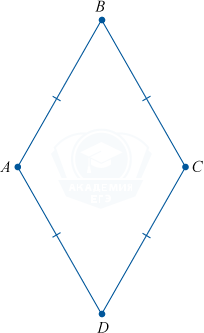
Ромб является частным случаем параллелограмма.
Ромб имеющий прямые углы является квадратом.
Содержание
СкрытьПоказатьСвойства ромба
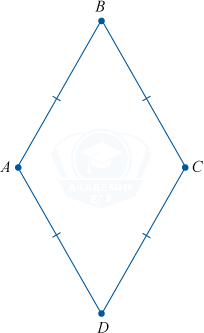
1. Противолежащие стороны ромба параллельны и равны.
AB \parallel CD,\;BC \parallel AD
AB = CD,\;BC = AD
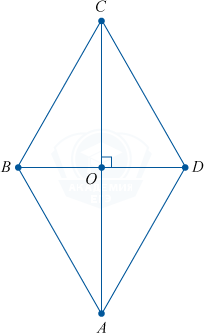
2. Диагонали ромба перпендикулярны.
AC\perp BD
Доказательство
Так как ромб является параллелограммом, то его диагонали делятся пополам.
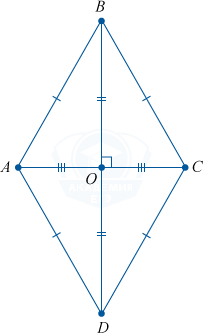
Значит, \triangle BOC = \triangle DOC по трем сторонам (BO = OD, OC — совместная, BC = CD). Получаем, что \angle BOC = \angle COD, и они смежны.
\Rightarrow \angle BOC = 90^{\circ} и \angle COD = 90^{\circ}.
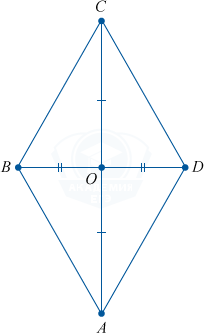
3. Точка пересечения диагоналей делит их пополам.
AC=2\cdot AO=2\cdot CO
BD=2\cdot BO=2\cdot DO
4. Диагонали ромба являются биссектрисами его углов.
\angle 1 = \angle 2; \; \angle 5 = \angle 6;
\angle 3 = \angle 4; \; \angle 7 = \angle 8.
Доказательство
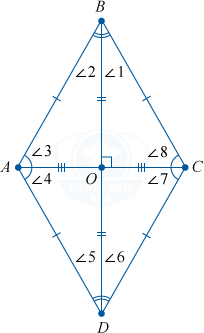
По причине того, что диагонали разделены точкой пересечения пополам, и все стороны ромба равны друг другу, то вся фигура делится диагоналями на 4 равных треугольника:
\triangle BOC, \; \triangle BOA, \; \triangle AOD, \; \triangle COD.
Это значит, что BD, AC — биссектрисы.
5. Диагонали образуют из ромба 4 прямоугольных треугольника.
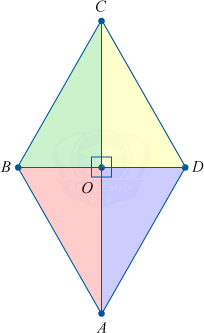
6. Любой ромб может содержать окружность с центром в точке пересечения его диагоналей.
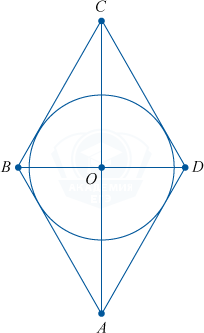
7. Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
AC^2 + BD^2 = 4\cdot AB^2
Признаки ромба
1. Параллелограмм с перпендикулярными диагоналями является ромбом.
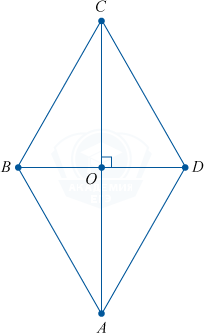
\begin{cases} AC \perp BD \\ ABCD \end{cases} — параллелограмм, \Rightarrow ABCD — ромб.
Доказательство
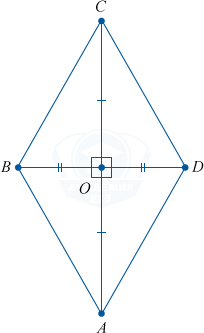
ABCD является параллелограммом \Rightarrow AO = CO; BO = OD. Также указано, что AC \perp BD \Rightarrow \triangle AOB = \triangle BOC = \triangle COD = \triangle AOD - по 2-м катетам.
Получается, что AB = BC = CD = AD.
Доказано!
2. Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то этой фигурой будет ромб.
Доказательство
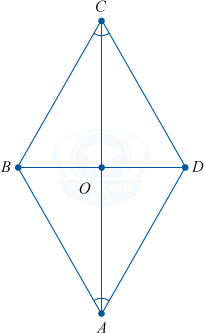
\angle A = \angle C, поскольку ABCD — параллелограмм. AC — биссектриса \angle A и \angle C.
Следовательно, \triangle ABC = \triangle ADC и оби фигуры — равнобедренные треугольники.
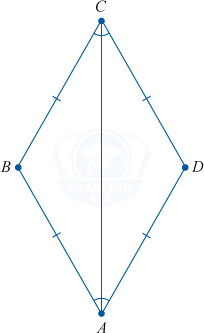
Это означает, что AB = BC = CD = DA, и ABCD — ромб.
На заметку: не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом.
К примеру:
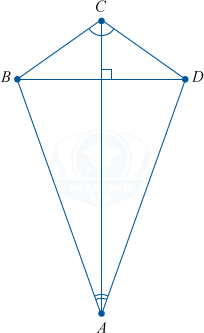
Это уже не ромб, не смотря на перпендикулярность диагоналей.
Для отличия стоит запомнить, что сначала четырехугольник должен быть параллелограммом и иметь признаки параллелограмма 1 и 2