Прямоугольник
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
.png)
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.
Свойства прямоугольника
1. Прямоугольник — это параллелограмм.
Доказательство
Свойство объясняется действием признака 3 параллелограмма (то есть \angle A = \angle C, \angle B = \angle D)
2. Противоположные стороны равны.
AB = CD,\enspace BC = AD

3. Противоположные стороны параллельны.
AB \parallel CD,\enspace BC \parallel AD
4. Прилегающие стороны перпендикулярны друг другу.
AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB

5. Диагонали прямоугольника равны.
AC = BD
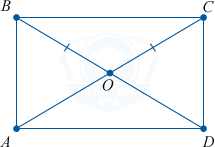
Доказательство
Согласно свойству 1 прямоугольник является параллелограммом, а значит AB = CD.
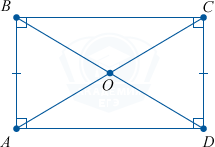
Следовательно, \triangle ABD = \triangle DCA по двум катетам (AB = CD и AD — совместный).
Если обе фигуры — ABC и DCA тождественны, то и их гипотенузы BD и AC тоже тождественны.
Значит, AC = BD.
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
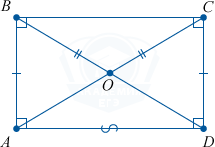
ABCD — параллелограмм \Rightarrow AB = CD, AC = BD по условию. \Rightarrow \triangle ABD = \triangle DCA уже по трем сторонам.
Получается, что \angle A = \angle D (как углы параллелограмма). И \angle A = \angle C, \angle B = \angle D.
Выводим, что \angle A = \angle B = \angle C = \angle D. Все они по 90^{\circ}. В сумме — 360^{\circ}.
Доказано!
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон.
Это свойство справедливо в силу теоремы Пифагора.
AC^2=AD^2+CD^2
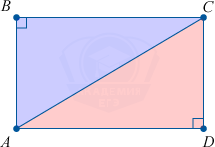
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника.
\triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD
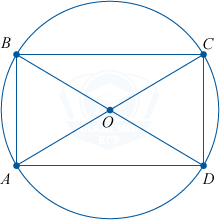
8. Точка пересечения диагоналей делит их пополам.
AO = BO = CO = DO
.png)
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности.
10. Сумма всех углов равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}
11. Все углы прямоугольника прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника.
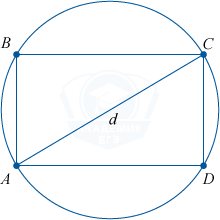
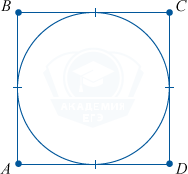
13. Вокруг прямоугольника всегда можно описать окружность.
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна 180^{\circ}
\angle ABC = \angle CDA = 180^{\circ},\enspace \angle BCD = \angle DAB = 180^{\circ}
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом).