Задание №238
Условие
Найдите все значения a, при каждом из которых система имеет единственное решение:
\begin{cases} (\left | x \right |-4)^{2}+(y-3)^{2}=2, \\ y=\left | x-1\right |+a.\end{cases}
Решение
Если x \geq 0, то уравнение (\left | x \right |-4)^{2}+(y-3)^{2}=2 задает окружность с центром C_{2}(4;3) радиусом \sqrt{2}. Если x < 0, то это уравнение задает окружность с центром C_{1}(-4;3) радиусом \sqrt{2}.
Второе уравнение y=\left | x-1\right |+a системы задает прямой угол с переменной вершиной (1;a), находящейся на прямой x=1.
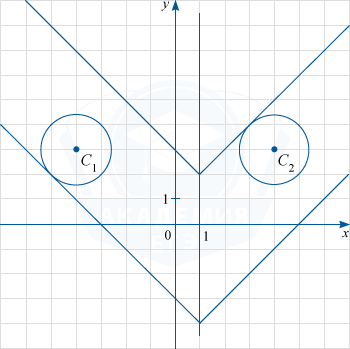
Графики этих уравнений имеют единственную общую точку тогда, когда одна сторона прямого угла касается одной из окружностей, а вторая сторона этого угла не имеет с окружностями общей точки. Это произойдет в двух случаях.
По рисунку видим, что при этом a=2 или a=-4. Проверим, что при этих значениях действительно прямая касается окружности.
1) a=2, тогда прямая y=x+1 и окружность (x-4)^{2}+(y-3)^{2}=2 имеют одну общую точку, потому что соответствующая им система уравнений
\begin{cases} (x-4)^{2}+(y-3)^{2}=2, \\ y=x+1\end{cases} имеет единственное решение (3;4).
2) a=-4, тогда прямая y=-x-3 и окружность (x+4)^{2}+(y-3)^{2}=2 имеют одну общую точку, потому что соответствующая им система уравнений \begin{cases}(x+4)^{2}+(y-3)^{2}=2, \\ y=-x-3 \end{cases} имеет единственное решение (-5;2).
Ответ
(-4;2)