Задание №204

а) 2\sin x+|\cos x|-3\cos x=0

1) \cos x\geqslant0, тогда |\cos x|=\cos x и уравнение примет вид

2\sin x+\cos x-3\cos x=0,

2\sin x-2\cos x=0,

\sin x=\cos x.

При \cos x\neq 0 имеем tg x=1, x=\frac{\pi}{4}+\pi n, n\in \mathbb{Z}.

Учитывая, что \cos \geqslant0, x=\frac{\pi}{4}+2\pi n, n\in \mathbb{Z} .

2) \cos x<0, тогда |\cos x|=-\cos x и уравнение примет вид

2\sin x-\cos x-3\cos x=0,

2\sin x-4\cos x=0,

\sin x=2\cos x.

При \cos x\neq 0 имеем tg x=2, x=arctg2+\pi k, k\in \mathbb{Z}.

Учитывая, что \cos <0, x=\pi+arctg2+2\pi k, k\in \mathbb{Z} или x=arctg2+\pi(1+2k), k\in \mathbb{Z} .

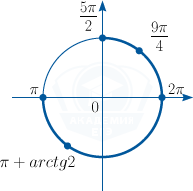
б) С помощью числовой окружности отберем корни, принадлежащие промежутку \left [\pi;\frac{5\pi}{2}\right].

x_1=2\pi+\frac{\pi}{4}=\frac{9\pi}{4};

x_2=\pi+arctg2.

а) \frac{\pi}{4}+2\pi n, n\in \mathbb{Z};\;arctg2+\pi(1+2k), k\in \mathbb{Z};

б) \pi+arctg2;\;\frac{9\pi}{4}.