Задание №165
Условие
а) Решите уравнение (16^{\sin x})^{\cos x}=\left ( \frac{1}{4} \right )^{\sqrt{3}\sin x}
б) Найдите все корни этого уравнения, принадлежащие отрезку \left [ 2\pi ; \frac{7\pi }{2} \right ]
Решение
a) Преобразуем уравнение:
4^{2\sin x\cdot \cos x}=4^{-\sqrt{3}\sin x}
2 \sin x \cdot cos x =-\sqrt{3}\sin x
\sin x=0 или \cos x=-\frac{\sqrt{3}}{2}
x=\pi R, R\in \mathbb{Z} или x=\pm \frac{5\pi}{6}+2\pi R, R\in \mathbb{Z}.
б) При помощи тригонометрической окружности отберем корни, принадлежащие заданному отрезку.
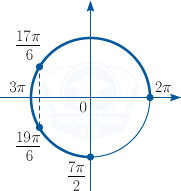
У нас получается: x=2\pi, x=\frac{17\pi}{6}, x=3\pi, x=\frac{19\pi}{6}.
Ответ
а) \pi R; \pm \frac{5\pi}{6}+2\pi R; R\in \mathbb{Z}. б) 2\pi; \frac{17\pi}{6}; 3\pi; \frac{19\pi}{6}.
Источник: «Математика ЕГЭ 2016. Типовые тестовые задания». Под ред. И. В. Ященко.
Константин Парфенов /