Задание №975

а) Используя формулы приведения и основное тригонометрическое тождество, преобразуем уравнение так, чтобы в нём была только одна тригонометрическая функция с одинаковым аргументом. Сделав замену \sin x=t, получим квадратное уравнение, решив которое, вернёмся к переменной x.

3-2(1-\sin^{2}x)+3 \sin (x-\pi)=0,

2\sin^{2}x-3\sin x+1=0.

Пусть \sin x=t, тогда 2t^{2}-3t+1=0,

t_{1}=1,  t_{2}=\frac{1}{2}.

\sin x=1, тогда x=\frac{\pi}{2}+2 \pi k, k \in \mathbb Z.

\sin x=\frac{1}{2}, тогда x=(-1)^{n}\frac{\pi}{6}+\pi n, n \in \mathbb Z.

б) Корни, принадлежащие промежутку \left [ \frac{7 \pi}{2}; \frac{11 \pi}{2}\right ), найдём с помощью тригонометрической окружности.

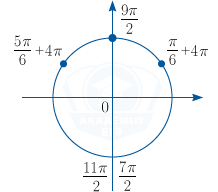
4\pi+\frac{\pi}{2}=\frac{9\pi}{2};

4\pi+\frac{\pi}{6}=\frac{25\pi}{6};

4\pi+\frac{5\pi}{6}=\frac{29 \pi}{6}.

а) \frac{\pi}{2}+2 \pi k, k \in \mathbb Z; (-1)^{n}\frac{\pi}{6}+\pi n, n \in \mathbb Z;

б) \frac{25\pi}{6}; \frac{9\pi}{2}; \frac{29 \pi}{6}