Дроби

Основное свойство дроби

Если ad=bc, то две дроби \frac{a}{b}и \frac{c}{d} считаются равными. К примеру, равными будут дроби \frac35и \frac{9}{15}, так как 3 \cdot 15 = 15 \cdot 9, \frac{12}{7}и \frac{24}{14}, так как 12 \cdot 14 = 7 \cdot 24.

Из определения равенства дробей следует, что равными будут дроби \frac{a}{b}и \frac{am}{bm}, так как a(bm)=b(am) — наглядный пример применения сочетательного и переместительного свойств умножения натуральных чисел в действии.

Значит \frac{a}{b} = \frac{am}{bm} — так выглядит основное свойство дроби.

Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.

Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.

Сокращать дроби принято, опираясь на основное свойство дроби.

Например, \frac{45}{60}=\frac{15}{20}(числитель и знаменатель делится на число 3); полученную дробь снова можно сократить, разделив на 5, то есть \frac{15}{20}=\frac 34.

Несократимая дробь — это дробь вида \frac 34, где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.

Приведение дробей к общему знаменателю

Возьмем в качестве примера две дроби: \frac{2}{3}и \frac{5}{8} с разными знаменателями 3 и 8. Для того, чтобы привести данные дроби к общему знаменателю и сначала перемножим числитель и знаменатель дроби \frac{2}{3}на 8. Получаем следующий результат: \frac{2 \cdot 8}{3 \cdot 8} = \frac{16}{24}. Затем умножаем числитель и знаменатель дроби \frac{5}{8}на 3. Получаем в итоге: \frac{5 \cdot 3}{8 \cdot 3} = \frac{15}{24}. Итак, исходные дроби приведены к общему знаменателю 24.

Арифметические действия над обыкновенными дробями

Сложение обыкновенных дробей

а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:

\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b};

б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а):

\frac{7}{3}+\frac{1}{4}=\frac{7 \cdot 4}{3}+\frac{1 \cdot 3}{4}=\frac{28}{12}+\frac{3}{12}=\frac{31}{12}.

Вычитание обыкновенных дробей

а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:

\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b};

б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а).

Умножение обыкновенных дробей

Умножение дробей подчиняется следующему правилу:

\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d},

то есть перемножают отдельно числители и знаменатели.

Например:

\frac{3}{5} \cdot \frac{4}{8} = \frac{3 \cdot 4}{5 \cdot 8}=\frac{12}{40}.

Деление обыкновенных дробей

Деление дробей производят следующим способом:

\frac{a}{b} : \frac{c}{d}= \frac{ad}{bc},

то есть дробь \frac{a}{b} умножается на дробь \frac{d}{c}.

Пример: \frac{7}{2} : \frac{1}{8}=\frac{7}{2} \cdot \frac{8}{1}=\frac{7 \cdot 8}{2 \cdot 1}=\frac{56}{2}.

Взаимно обратные числа

Если ab=1, то число b является обратным числом для числа a.

Пример: для числа 9 обратным является \frac{1}{9}, так как 9 \cdot \frac{1}{9}=1, для числа 5 — \frac{1}{5}, так как 5 \cdot \frac{1}{5}=1.

Десятичные дроби

Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10\,000, ..., 10^n.

Например: \frac{6}{10}=0,6;\enspace \frac{44}{1000}=0,044.

Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.

Например: 5\frac{1}{10}=5,1;\enspace \frac{763}{100}=7\frac{63}{100}=7,63.

В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10.

Пример: 5 — делитель числа 100, поэтому дробь \frac{1}{5}=\frac{1 \cdot 20}{5 \cdot 20}=\frac{20}{100}=0,2.

Арифметические действия над десятичными дробями

Сложение десятичных дробей

Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.

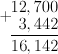
Вычитание десятичных дробей

Выполняется аналогично сложению.

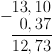
Умножение десятичных дробей

При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.

Давайте выполним умножение 2,7 на 1,3. Имеем 27 \cdot 13=351. Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=2). В итоге получаем 2,7 \cdot 1,3=3,51.

Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

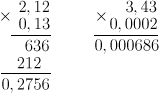
Для умножения на 10, 100, 1000, надо в десятичной дроби перенести запятую на 1, 2, 3 цифры вправо (в случае необходимости справа приписывается определенное число нулей).

Например: 1,47 \cdot 10\,000 = 14 700.

Деление десятичных дробей

Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.

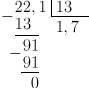
Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:

Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Первым делом, умножим делимое и делитель дроби на 100, то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112, то есть задача сводится к уже рассмотренному случаю:

Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.

2,8 : 0,09= \frac{28}{10} : \frac {9}{100}= \frac{28 \cdot 100}{10 \cdot 9}=\frac{280}{9}=31 \frac{1}{9}.