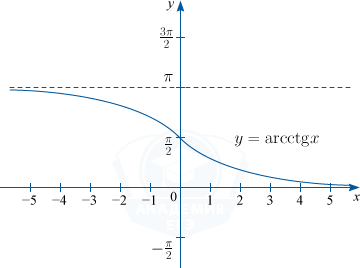Функция. Область определения и область значений функции. Графики функции

Графики элементарных функций

Линейная функция

Линейная функция — это функция вида y=kx+b, где k и b некоторые действительные числа.

Если b=0, то функция примет вид y=kx и будет называться прямой пропорциональностью.

D(f) : x \in R;\enspace E(f) : y \in R

График линейной функции — прямая.

Угловой коэффициент k прямой y=kx+b вычисляется по следующей формуле:

k= tg \alpha , где \alpha — угол наклона прямой к положительному направлению оси Ox.

1) Функция монотонно возрастает при k > 0.

Например: y=x+1

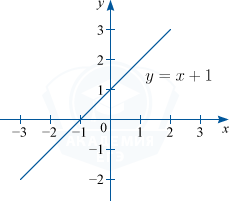
2) Функция монотонно убывает при k < 0.

Например: y=-x+1

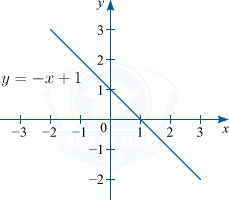
3) Если k=0, то придавая b произвольные значения, получим семейство прямых параллельных оси Ox.

Например: y=-1

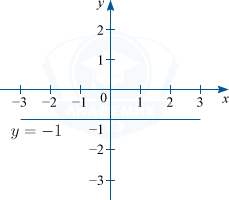
Обратная пропорциональность

Обратной пропорциональностью называется функция вида y=\frac {k}{x}, где k — отличное от нуля, действительное число

D(f) : x \in \left \{ R/x \neq 0 \right \}; \: E(f) : y \in \left \{R/y \neq 0 \right \}.

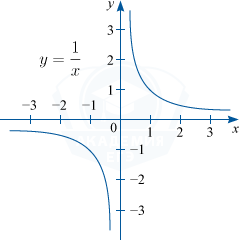
Графиком функции y=\frac {k}{x} является гипербола.

1) Если k > 0, то график функции будет располагаться в первой и третьей четверти координатной плоскости.

Например: y=\frac{1}{x}

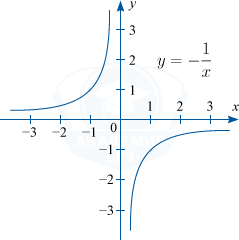
2) Если k < 0, то график функции будет располагаться во второй и четвертой координатной плоскости.

Например: y=-\frac{1}{x}

Степенная функция

Степенная функция — это функция вида y=x^n, где n — отличное от нуля, действительное число

1) Если n=2, то y=x^2. D(f) : x \in R; \: E(f) : y \in [0; +\infty) .

Графиком функции y=x^2 является парабола.

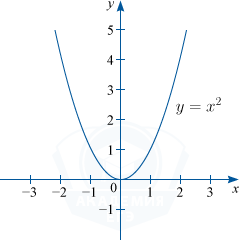
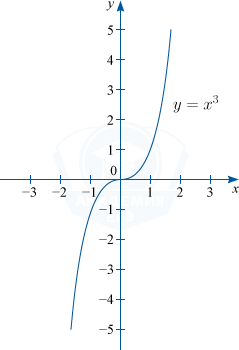
2) Если n=3, то y=x^3. D(f) : x \in R; \: E(f) : y \in R .

Графиком функции y=x^3 является кубическая парабола.

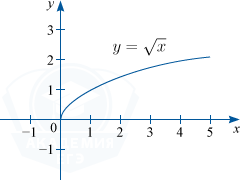
3) Если n=\frac{1}{2}, то y=x^\tfrac{1}{2} или y=\sqrt{x}. D(f) : x \in [0; +\infty ); \: E(f) : y \in [0; +\infty )

4) Если n=\frac{1}{3}, то y=x^\tfrac{1}{3} или y=\sqrt[3]{x}. D(f) : x \in R; \: E(f) : y \in R

Показательная функция

Показательная функция — это функция вида y=a^x, где a=const, a > 0, a \neq 1

D(f) : x \in R; \: E(f) : y \in (0; +\infty ).

Графиком показательной функции является экспонента.

1) Функция будет монотонно возрастать при a > 1.

Например: y=2^x

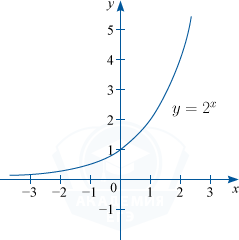
2) Функция монотонно убывает при 0 < a < 1.

Например: y=\left (\frac{1}{2} \right )^{x}

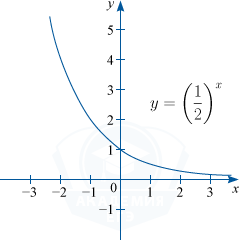
Логарифмическая функция

Логарифмическая функция — это функция вида y=\log_{a}x, где a — действительное число, a > 0, \: a \neq 1

D(f) : x \in (0; +\infty ); \: E(f) : y \in R.

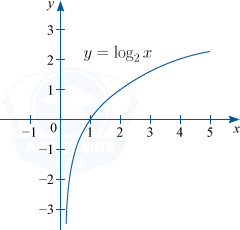
1) Функция монотонно возрастает при a > 1.

Например: y=\log_{2}x

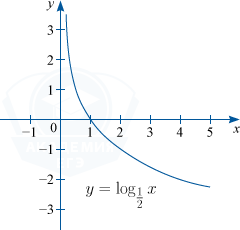
2) Функция будет монотонно убывать при 0 < a < 1.

Например: y=\log_{\tfrac{1}{2}}x

Тригонометрическая функция

К тригонометрическим функциям относят функции вида:

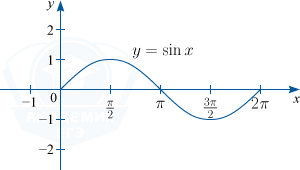
1) y=\sin x. D(f) : x \in R; \: E(f) : y \in [-1; 1]; основной период функции T=2 \pi

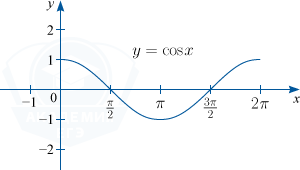
2) y = \cos x. D(f) : x \in R; \: E(f) : y \in [-1; 1]; основной период функции T=2 \pi

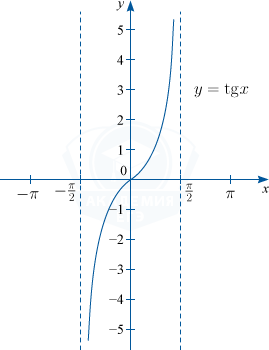
3) y = tg x. D(f) : x \in \left \{ R /x \neq \frac{\pi}{2}+\pi n\right \}, n \in \mathbb{Z}; \: E(f) : y \in R; основной период функции T= \pi

4) y = ctg x. D(f) : x \in \left \{ R /x \neq 0+\pi n\right \}, n \in \mathbb{Z}; \: E(f) : y \in R; основной период функции T= \pi

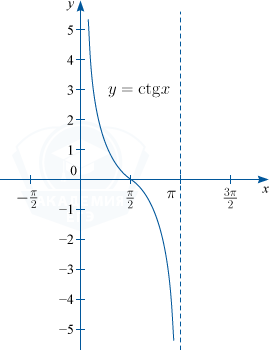
Обратные тригонометрические функции

К обратным тригонометрическим функциям относят функции вида:

1) y=\arcsin x. D(f) : x \in [-1; 1], \: E(f) : y \in \left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]

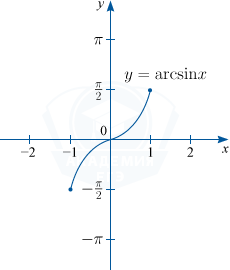
2) y=arccos x. D(f) : x \in [-1; 1], \: E(f) : y \in [0; \pi]

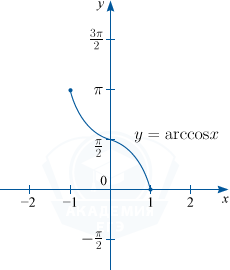
3) y=arctg x. D(f) : x \in R, \: E(f) : y \in \left (-\frac{\pi}{2}; \frac{\pi}{2} \right )

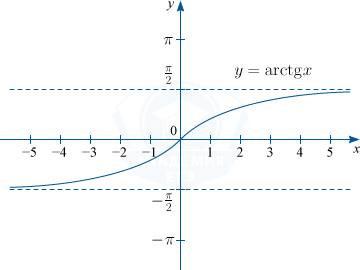
4) y= arcctg x. D(f) : x \in R, \: E(f) : y \in \left (0; \pi \right )