Четность и нечетность функции. Период функции. Экстремумы функции

Способы задания функции

Пусть функция задается формулой: y=2x^{2}-3. Назначая любые значения независимой переменной x, можно вычислить, пользуясь данной формулой соответствующие значения зависимой переменной y. Например, если x=-0,5, то, пользуясь формулой, получаем, что соответствующее значение y равно y=2 \cdot (-0,5)^{2}-3=-2,5.

Взяв любое значение, принимаемое аргументом x в формуле y=2x^{2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x. Наиболее часто, это будет приближенное значение функции.

Четная и нечетная функция

Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy.

Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. Такая функция будет симметрична относительно начала координат O (0;0).

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

f(x)=3x^{3}-7x^{7}

D(f)=(-\infty ; +\infty ) с симметричной областью определения относительно начала координат. f(-x)= 3 \cdot (-x)^{3}-7 \cdot (-x)^{7}= -3x^{3}+7x^{7}= -(3x^{3}-7x^{7})= -f(x).

Значит, функция f(x)=3x^{3}-7x^{7} является нечетной.

Периодическая функция

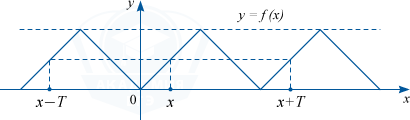
Функция y=f(x), в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x), называется периодической функцией с периодом T \neq 0.

Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T.

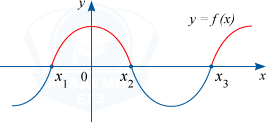
Промежутки, где функция положительная, то есть f(x) > 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.

f(x) > 0 на (x_{1}; x_{2}) \cup (x_{3}; +\infty )

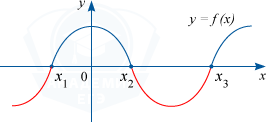
Промежутки, где функция отрицательная, то есть f(x) < 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x) < 0 на (-\infty; x_{1} ) \cup (x_{2}; x_{3} )

Ограниченность функции

Ограниченной снизу принято называть функцию y=f(x), x \in X тогда, когда существует такое число A, для которого выполняется неравенство f(x) \geq A для любого x \in X.

Пример ограниченной снизу функции: y=\sqrt{1+x^{2}} так как y=\sqrt{1+x^{2}} \geq 1 для любого x.

Ограниченной сверху называется функция y=f(x), x \in X тогда, когда существует такое число B, для которого выполняется неравенство f(x) \neq B для любого x \in X.

Пример ограниченной снизу функции: y=\sqrt{1-x^{2}}, x \in [-1;1] так как y=\sqrt{1+x^{2}} \neq 1 для любого x \in [-1;1].

Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0, для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X.

Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1.

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).

а) Если при x > 0 четная функция возрастает, то убывает она при x < 0

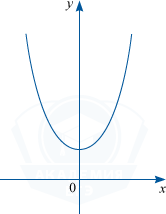
б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0

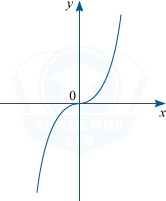
г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0

Экстремумы функции

Точкой минимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняться неравенство f(x) > f(x_{0}). y_{min} - обозначение функции в точке min.

Точкой максимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняется неравенство f(x) < f(x^{0}). y_{max} - обозначение функции в точке max.

Необходимое условие

Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x), что дифференцируема в точке x_{0}, появится экстремум в этой точке.

Достаточное условие

1. Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
2. x_{0} - будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}.

Наибольшее и наименьшее значение функции на промежутке

Шаги вычислений:

1. Ищется производная f'(x);
2. Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b];
3. Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.